Permutation: Arrangement without repetition
LIKE TO JOIN ON FACEBOOK (click here)
Permutation: Permutations enables us to find the numer of ways of arranging a set of objects, some of which may be identical. Any particular arrangement of the set of objects will be one permutation out of all the possible permutations. In permutation order is important as it is basically the number of ways of arrangement of a set of objects.
1. Arrangement without Repetition:
a. Order is important
Sometimes we have to arrange objects where order is important
e.g. 1,2,3
if we place these three numbers in different orders we get different results as 123 and 321. Therefore, here order is important.
b. Without Repetition ( Objects are distinct )
i.e. without repetition means in a particular arrangement all objects are different
e.g. here some objects are repeated 112 , 222, 333, 121
Recall the product rule: for every choice of first place, there are four choices to select the letter for second place, and so on.
Therefore, total number of arrangements = = 120
= 120
5! called as 5 factorial
and , 5! = 5*4*3*2*1
7! = 7*6*5*4*3*2*1
So if we generalise the above example i.e. we have to arrange n distinct objects, the number of ways = n!
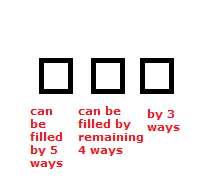
Now if we have to make three letter words out of five letters a,b,c,d and e
So we have three places, first place can be filled by 5 ways, 2nd by 4 ways and 3rd or last by 3 ways,
Therefore, total number of ways or total number of three letter words having different letters formed by the given 5 letters = 5 * 4 * 3 = 60
=
 - Number of ways of Arranging 'n' things, taken 'r' at a time
- Number of ways of Arranging 'n' things, taken 'r' at a time
So, there are r places and n objects,
1st place can be filled by n ways, 2nd by (n - 1), 3rd by (n - 2) and so on. And rth place can be filled by (n - r + 1) ways,
therefore,

or,
or,
Ques: How many words can be made of letters COURTESY which began with C and end with Y ?
Sol: Since first letter C and last letter Y are fixed. Therefore we have to permutate only six letters between C and Y,
C O U R T E S Y
Therefore, total number of words = = 6! = 720
= 6! = 720
Ques: Of 8 balls how many arrangement can be made in which 3 given balls are not all together ?
Sol: We must first determine the number of ways in which three given balls can be arranged together, and then subtract that number by the total number of ways in which these eight balls can be arranged, to obtain the number of ways in which three given balls are not all together.
Permutation: Permutations enables us to find the numer of ways of arranging a set of objects, some of which may be identical. Any particular arrangement of the set of objects will be one permutation out of all the possible permutations. In permutation order is important as it is basically the number of ways of arrangement of a set of objects.
1. Arrangement without Repetition:
a. Order is important
Sometimes we have to arrange objects where order is important
e.g. 1,2,3
if we place these three numbers in different orders we get different results as 123 and 321. Therefore, here order is important.
b. Without Repetition ( Objects are distinct )
i.e. without repetition means in a particular arrangement all objects are different
e.g. here some objects are repeated 112 , 222, 333, 121
Let's look at an example. Suppose we need to create five-letter words from the letters a, b, c, d, and e. Therefore, the question is how many words with distinct letters we can create, or how many different ways there are to arrange five letters without repeating any of them.
There are five places where we need to put these five different letters.
There are five ways to get to first place. ( i.e. a or b or c or d or e )
When we choose a letter for the first spot, we can't use it again, so we're only left with four letters. There are four ways to fill the second spot. In the same way, there are three ways to fill 3rd place, two ways to fill 4th place, and only one way to fill 5th place.
Recall the product rule: for every choice of first place, there are four choices to select the letter for second place, and so on.
Therefore, total number of arrangements =
5! called as 5 factorial
and , 5! = 5*4*3*2*1
7! = 7*6*5*4*3*2*1
So if we generalise the above example i.e. we have to arrange n distinct objects, the number of ways = n!
Now if we have to make three letter words out of five letters a,b,c,d and e
So we have three places, first place can be filled by 5 ways, 2nd by 4 ways and 3rd or last by 3 ways,
Therefore, total number of ways or total number of three letter words having different letters formed by the given 5 letters = 5 * 4 * 3 = 60
=
So, there are r places and n objects,
1st place can be filled by n ways, 2nd by (n - 1), 3rd by (n - 2) and so on. And rth place can be filled by (n - r + 1) ways,
therefore,
or,
or,
Ques: How many words can be made of letters COURTESY which began with C and end with Y ?
Sol: Since first letter C and last letter Y are fixed. Therefore we have to permutate only six letters between C and Y,
C O U R T E S Y
Therefore, total number of words =
Ques: Of 8 balls how many arrangement can be made in which 3 given balls are not all together ?
Sol: We must first determine the number of ways in which three given balls can be arranged together, and then subtract that number by the total number of ways in which these eight balls can be arranged, to obtain the number of ways in which three given balls are not all together.
Number of ways in which 3 given balls are not all together =
Total Number of ways - Number of ways in which 3 given balls are together
for total number of ways i.e. arranging 8 balls in 8 places
Total number of ways =
for the number of ways in which three given balls can be arranged together, we knot the three balls together and regard them as ONE ball, we now have 6 balls, and the total number of ways to arrange them is
But we can also arrange these 3 given balls in
Therefore,
Number of ways in which 3 given balls are together =
Therefore,
Number of ways in which 3 given balls are not all together = 8! - 6!.3!
Ques: A self conains 20 books 4 are single volume and others forms sets of 8, 5 and 3 volumes respectively. Find how many ways the books can arrange in the self so that the volume of these sets are together and will be in order ?
Sol: There are 20 books and there are also three sets of books having 8, 5 and 3 volumes.
Since we have to place the volumes of these sets together, therefore we have to treat the bundle of the same volumes of sets as one book.
Therefore, now we have to place 7 books in 7 places
Therefore, number of ways to place these books in self =
but these volumes should be in order and can place in two ways i.e. in descending order or ascending order
e.g. vol. 1 vol. 2 vol. 3
or vol. 3 vol. 2 vol. 1
and there are three sets having volumes,
So, total number of ways these books in shelf having the volumes are together and in order = 7!*2*2*2
LIKE TO JOIN ON FACEBOOK (click here)


Comments
Post a Comment