Solved Examples - II: Complex Number

By -
LIKE TO JOIN ON FACEBOOK (click here)



Ques: Show that all the roots of the equation {a_1}{z^3} + {a_2}{z^2} + {a_3}z + {a_4} = 3 where |{a_i}| \le 1 ; i = 1,2,3,4 lie outside the circle |z| = 2/3 ?
Solution: For proving the above problem, first we assume the contrary of the same that roots of the equation lie inside or 'on' the circle i.e.  |z| \le \frac{2}{3} , 

 Now,

 {a_1}{z^3} + {a_2}{z^2} + {a_3}z + {a_4} = 3

 \Rightarrow {a_1}{z^3} + {a_2}{z^2} + {a_3}z = 3 - {a_4}

 Taking mod of both the sides,

 \Rightarrow \left| {3 - {a_4}} \right| = \left| {{a_1}{z^3} + {a_2}{z^2} + {a_3}z} \right|

 (for properties of modulus of complex number [click here] )

 or, \left| {3 - {a_4}} \right| \le |{a_1}||z{|^3} + |{a_2}||z{|^2} + |{a_3}||z|   ( since |x + y + z| \le |x| + |y| + |z| )

 [ since |{a_i}| \le 1; i = 1,2,3,4 , therefore |{a_1}||z{|^3} + |{a_2}||z{|^2} + |{a_3}||z| \le |z{|^3} + |z{|^2} + |z|  ]

 or, \left| {3 - {a_4}} \right| \le |z{|^3} + |z{|^2} + |z|

 or, \left| {3 - {a_4}} \right| \le |z|\left( {\frac{{|z{|^3} - 1}}{{|z| - 1}}} \right)  ( by sum of Geometric Progression )

 Now, \left| {3 - {a_4}} \right| \ge \left| {3 - |{a_4}|} \right|  as, |{a_4}| \le 1

\Rightarrow \left| {3 - |{a_4}|} \right| \le \left| {3 - {a_4}} \right| \le |z|\left( {\frac{{|z{|^3} - 1}}{{|z| - 1}}} \right)

but we assume that |z| \le \frac{2}{3}

 \Rightarrow \left| {3 - |{a_4}|} \right| \le |z|\left( {\frac{{|z{|^3} - 1}}{{|z| - 1}}} \right)| \le \frac{2}{3}\left( {\frac{{{{\left( {\frac{2}{3}} \right)}^3} - 1}}{{\frac{2}{3} - 1}}} \right)

\Rightarrow \left| {3 - |{a_4}|} \right| \le \frac{{38}}{{27}} \sim 1.4  ( Less than or equal to 1.4 ) ............ (i)

 but \left| {3 - |{a_4}|} \right| \ge |3 - 1| = 2 ( greater than or equal to 2 ) ..............(ii)

 from (i) and (ii), it is a contradiction. Hence |z| \le \frac{2}{3} is not true.
Therefore |z| = 2/3 and hence roots are lie outside the circle |z| = 2/3 ( Hence Proved )




Ques: Find the locus of z : {\log _{\sqrt 3 }}\frac{{|z{|^2} - |z| + 1}}{{|z| + 2}} < 2


Solution: {\log _{\sqrt 3 }}\frac{{|z{|^2} - |z| + 1}}{{|z| + 2}} < 2

 \Rightarrow \frac{{|z{|^2} - |z| + 1}}{{|z| + 2}} < {(\sqrt 3 )^2}  ( since base of log is greater than 1 therefore inequality would not get changed)

 \Rightarrow |z{|^2} - |z| + 1 < 3|z| + 6  ( since denominator was positive equality would not get changed )

 \Rightarrow |z{|^2} - 4|z| - 5 < 0

or, (|z| - 5)(|z| + 1) < 0

 But since |z| + 1 > 0

 Therefore, |z| - 5 < 0

 or, |z| < 5 

 Therefore locus of the z is region under the circle |z| = 5.




Ques: If non-zero complex numbers z1, z2 & z3 are in Harmonic Progression & at least one is not real then prove that z1, z2 & z3 lie on a circle passing through the origin ?
Solution:  Since, z1, z2 and z3 are in Harmonic Progression

 Therefore, \frac{2}{{{z_2}}} = \frac{1}{{{z_1}}} + \frac{1}{{{z_3}}} or \frac{1}{{{z_2}}} - \frac{1}{{{z_1}}} = \frac{1}{{{z_3}}} - \frac{1}{{{z_2}}}


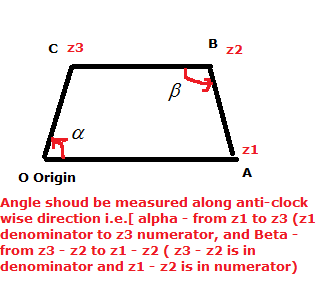
We know that for a cyclic quadrilateral, sum of opposite angles of quadrilateral is equal to Pi

 From figure, if we prove,  \alpha + \beta = \pi  then OABC would be a cyclic quadrilateral
i.e. \arg .\left( {\frac{{{z_3}}}{{{z_1}}}} \right) + \arg .\left( {\frac{{{z_1} - {z_2}}}{{{z_3} - {z_2}}}} \right) = \pi  then OABC would be a cyclic quadrilateral

 since,

 \frac{1}{{{z_2}}} - \frac{1}{{{z_1}}} = \frac{1}{{{z_3}}} - \frac{1}{{{z_2}}}     (since z1, z2 and z3 are in H.P. )

 or, \frac{{{z_1} - {z_2}}}{{{z_1}{z_2}}} = \frac{{{z_2} - {z_3}}}{{{z_3}{z_2}}}

 or, \frac{{{z_1}}}{{{z_3}}} = \frac{{{z_1} - {z_2}}}{{{z_2} - {z_3}}}

 or, \frac{{{z_1}}}{{{z_3}}} = ( - 1)\frac{{{z_1} - {z_2}}}{{{z_3} - {z_2}}}

 Therefore,

 \arg .\frac{{{z_1}}}{{{z_3}}} = \arg .\left[ {( - 1)\left( {\frac{{{z_1} - {z_2}}}{{{z_3} - {z_2}}}} \right)} \right]

(for properties of argument of complex number [click here] )

 or,  \arg .\frac{{{z_1}}}{{{z_3}}} = \arg .( - 1) + \arg .\left( {\frac{{{z_1} - {z_2}}}{{{z_3} - {z_2}}}} \right)   

 or,  - \arg .\frac{{{z_3}}}{{{z_1}}} = \pi + \arg .\left( {\frac{{{z_1} - {z_2}}}{{{z_3} - {z_2}}}} \right)  ( since arg (-1) = pi and \arg .\frac{{{z_1}}}{{{z_3}}} = - \arg .\frac{{{z_3}}}{{{z_1}}}  as,                                                                                                                         \arg .\frac{{{z_1}}}{{{z_3}}} = \arg {z_1} - \arg {z_3} )

 or, \arg .\left( {\frac{{{z_3}}}{{{z_1}}}} \right) + \arg .\left( {\frac{{{z_1} - {z_2}}}{{{z_3} - {z_2}}}} \right) = \pi

or, \alpha + \beta = \pi

Therefore quadrilateral OABC is cyclic ( Hence Proved)
LIKE TO JOIN ON FACEBOOK (click here)

Comments

Post a Comment

Popular posts from this blog

Properties of Modulus & Argument: Complex Number

By -
Image
Properties of Modulus: Modulus of z is the length of vector representing z form origin to the point z. 1.  If z = x + iy then   2.   &  Since,  ( equality follows when y = 0) and   (equality follows when x = 0) IMP 3.  Since, and,  4.  ,  5.  6.  7.   holds when  i.e. both the vectors are in same direction.  holds when   i.e. both the vectors are in opposite direction In general, 8.  IMP 9.  Explanation: Since,  Therefore,  or,                                                  [Since   (? click here ) ] and  10.     ( Property of Parallelogram ) Properties of Argument: Argument is the angle between the vector representing z from ...
Read more

Fractional Part function

By -
Image
10. Fractional Part f(x) = {x}  Every number 'x' can be written as the sum of its integer and fractional parts. x = [x] + {x} Therefore fractional part, {x} = x - [x] For example, 4.7 = 4 + 0.7 or, 0.7 = 4.7 - 4 i.e. fractional part = Number - Integral Part x = 4.7 , [x] = [4.7] = 4 and {x} = {4.7} = 0.7 Consider, {-4.7} {-4.7} = -4.7 - [-4.7] = -4.7 - (-5)  or, {-4.7} = 0.3 if the number is integer, its fractional part is obviously zero. {6} = 6 - [6] = 6 - 6 = 0 Note- fractional part is always positive and it never becomes 1. in other words, fractional part of a number is the difference between the number and its integral part. Remember,  i.e. fractional part is always less than 1 and greater than or equal to zero. When x will be an integer fractional part will become zero i.e. integer has no fractional part. How to draw the graph, note this, , if  because the fractional part is equal to the number if n...
Read more

Geometrical Meaning of Argument and Modulus - I: Complex Number

By -
Image
LIKE TO JOIN ON FACEBOOK ( click here ) Students are requested to understand this carefully   1. Arg(z) = pi/3 z = 0 is excluded since z = 0 is the only complex number whose argument is not defined 2. Arg(z) > pi/3 Since principal argument belongs to (-pi, pi],  therefore Argument cannot be greater than pi. therefore Arg(z) > pi/3 =>)  z = 0 is excluded 3. |Arg(z)| < pi/4 => -pi/4 < Arg(z) < pi/4 z = 0 is excluded 4. => Arg(z) = pi since, principal argument belongs to  , therefore Argument cannot be greater than pi. z = 0 is excluded 5.  -pi/3 is included z = 0 is excluded 6. Complex number   , equal only when z is purely real number or '0' IMP 7. Arg(|z|) = 0 Since |z| is a Positive Real number , therefore it lies on right side of x - axis i.e. on positive Real axis and x-axis has '0' argument because it makes 0 radian angle from x-axis For z = 0 , argument ...
Read more