Modulus of Quadratic Expression

By abhijatindia - March 13, 2013

We Know that,

| x |

of a real number

x

is the non-negative value of

x

without regard to its sign.

means,
if, y = |x|

,
$|x| \ge 0$
or we can say that ,
$y \ge 0$

means no part of the graph of |x| will be below the x-axis.

Actually, this is true for any f(x)

,
if

,

means no part of curve will below the x - axis, since $y \ge 0$

for, y = x

means if , $\begin{array}{l} x = 1 \Rightarrow y = 1\\ x = - 2 \Rightarrow y = - 2\\ x = - 1 \Rightarrow y = - 1 \end{array}$

and for , y = |x|

$\begin{array}{l} x = 1 \Rightarrow y = 1\\ x = - 2 \Rightarrow y = 2\\ x = - 1 \Rightarrow y = 1 \end{array}$

in |x| graph we can see from the figure that no part of curve will be on negative side of y- axis.

In fact we take the mirror image or reflection of negative side of y - axis in respect of x - axis and leave the part of negative side of y -axis.

Similarly if we have any y = |f(x)|

,
we will take the mirror image of part of negative side of y - axis about the x -axis and leave the part of negative side of y - axis or left the part of curve which is below the x -axis after taking the reflection,

or , we can say that the part of curve which is below to the x - axis, we multiply with it negative sign to make the part positive......

consider, y = |x|

for $x \le 0$ , part of y = x

is negative

therefore to make it positive we have to multiply it with -1

therefore,
y = |x| = x

, if $x \ge 0$

and y = |x| = - x

, if $x \le 0$

FROM ABOVE ARGUMENTS,

if we have,

$y = |a{x^2} + bx + c|$
i.e. f(x)

is a quadratic expression,

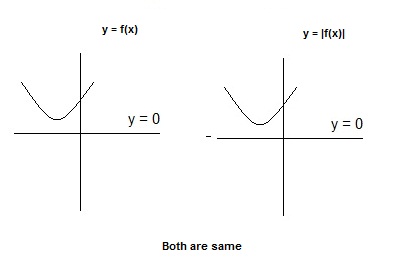
1st Condition,

if, a > 0

and

concave upward and no real roots (imaginary roots)
( previous post http://iitmathseasy.blogspot.in/2013/03/quadratic-expression-concept-ii.html)

therefore,
f(x) > 0

or, $(a{x^2} + bx + c) > 0$

since $a{x^2} + bx + c$ is always greater than '0'
and mod of any positive number is that number,

$\Rightarrow$ $y = |a{x^2} + bx + c| = a{x^2} + bx + c$

e.g. $y = |2{x^2} + 5x + 7|$

since a > 0

and

$\Rightarrow y = 2{x^2} + 5x + 7$

2nd Condition,

$y = |a{x^2} + bx + c|$

if, a < 0

and

curve is concave downwards and no real roots
( previous post http://iitmathseasy.blogspot.in/2013/03/quadratic-expression-concept-ii.html)

$\Rightarrow f(x) < 0$ or, $(a{x^2} + bx + c) < 0$

Since $a{x^2} + bx + c$ is always less than zero that is negative.
So, we have to make it positive by multiplying with -1.

$\Rightarrow y = |a{x^2} + bx + c| = - (a{x^2} + bx + c)$

3rd Condition,

$y = |a{x^2} + bx + c|$

a > 0

and

curve is concave upwards and have real roots means it will cut x-axis on two points (suppose ${x_1}$ and ${x_2}$ )

here use the method of solving modulus equation ( http://iitmathseasy.blogspot.in/2013/03/modulus-equality-solving-concept.html) step by step

starting from left,

i) $x \le {x_1}$ ,
from figure,

$y = |a{x^2} + bx + c| = a{x^2} + bx + c$

because for $x \le {x_1}$ , curve is positive

ii) ${x_1} \le x \le {x_2}$
from figure,

$\Rightarrow y = |a{x^2} + bx + c| = - (a{x^2} + bx + c)$

in this interval curve is negative, so we have to multiply by -1.

iii) $x \ge {x_2}$

from figure,

$y = |a{x^2} + bx + c| = a{x^2} + bx + c$

curve is positive.

4th condition,

$y = |a{x^2} + bx + c|$

a < 0,D > 0

concave downwards two real roots,

from the above arguments clear from figure.

i) $x \le {x_1}$

$\Rightarrow y = |a{x^2} + bx + c| = - (a{x^2} + bx + c)$

ii) ${x_1} \le x \le {x_2}$

$y = |a{x^2} + bx + c| = a{x^2} + bx + c$

iii) $x \ge {x_2}$

$\Rightarrow y = |a{x^2} + bx + c| = - (a{x^2} + bx + c)$

Search This Blog

Mathematics

Modulus of Quadratic Expression

Comments

Post a Comment

Popular posts from this blog

Properties of Modulus & Argument: Complex Number

Fractional Part function

Geometrical Meaning of Argument and Modulus - I: Complex Number